今回は3次元の図を描いてみましょう。
そこまで難しくはないと思います。
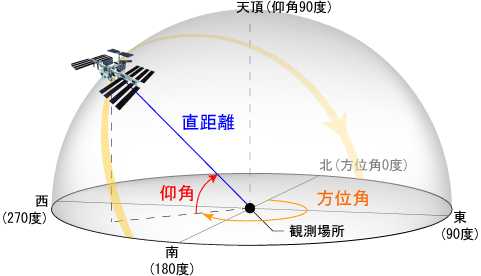
方位角と仰角
-p[方位角]/[仰角]/[基準座標]
※ 基準座標は0にしておいたほうが無難
3次元の図を描く際には -p をつける必要があります。
方位角 : 地平線の北方向から地平線に沿って時計回りに計った角度
仰角 : 地平線から天頂に向かって計った角度
補足説明 - 「きぼう」を見よう http://kibo.tksc.jaxa.jp/appendix.html より引用。
おすすめの角度は方位角220度、仰角20度です。何となくですが。
スクリプト上では -p220/20/0 となります。
図の枠を描く

gmt basemapの使い方
GMTのbasemapモジュールについて説明しています。
グラフも地図も書き方は一緒です。
gmt basemap -J[投影法][ヨコの長さ]/[タテの長さ] -JZ[Z軸の長さ] -R[南端]/[北端]/[西端]/[東端]/[Z軸最小値]/[Z軸最大値] -B[x|y|z][afg][+l"label"] -B[WSNEZ+t"title"] -p[方位角]/[仰角]/[基準座標]
※ -Bafg は -Bxyafg の略。
※ 基準座標は0にしておいたほうが無難
たとえば、XYZ軸ともに12cmかつ、0から10までの枠を描くには、
#!/bin/bash
gmt begin hogehoge jpg
gmt basemap -JX12 -JZ12 -R0/10/0/10/0/10 -Bafg -Bzafg -BWSneZ -p220/20/0
gmt endとすれば、
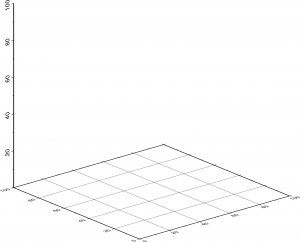
となります。
2次元のグラフや地図を描く際に使う-Bafg は -Bxafg -Byafgの省略形になります。
Z軸の目盛りも自動にする場合は、-Bzafg と別途で書く必要があります。
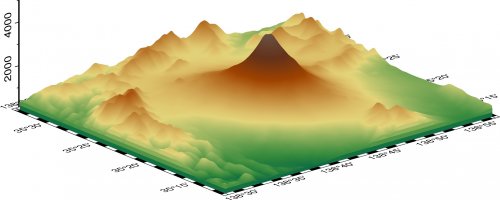
応用編
螺旋(helix)の座標データを作成する。
今回はPython3で作ってみた。
import math
r = 4
for i in range(0, 1440):
rad = math.radians(i)
x = r * math.cos(rad) + 5
y = r * math.sin(rad) + 5
z = i * 0.005
with open("plot.txt", mode='a') as f:
f.write(str(x) + "," + str(y) + "," + str(z) + "\n")これで(5,5)を中心とする半径4の螺旋の座標データ、plot.txt が出力される。
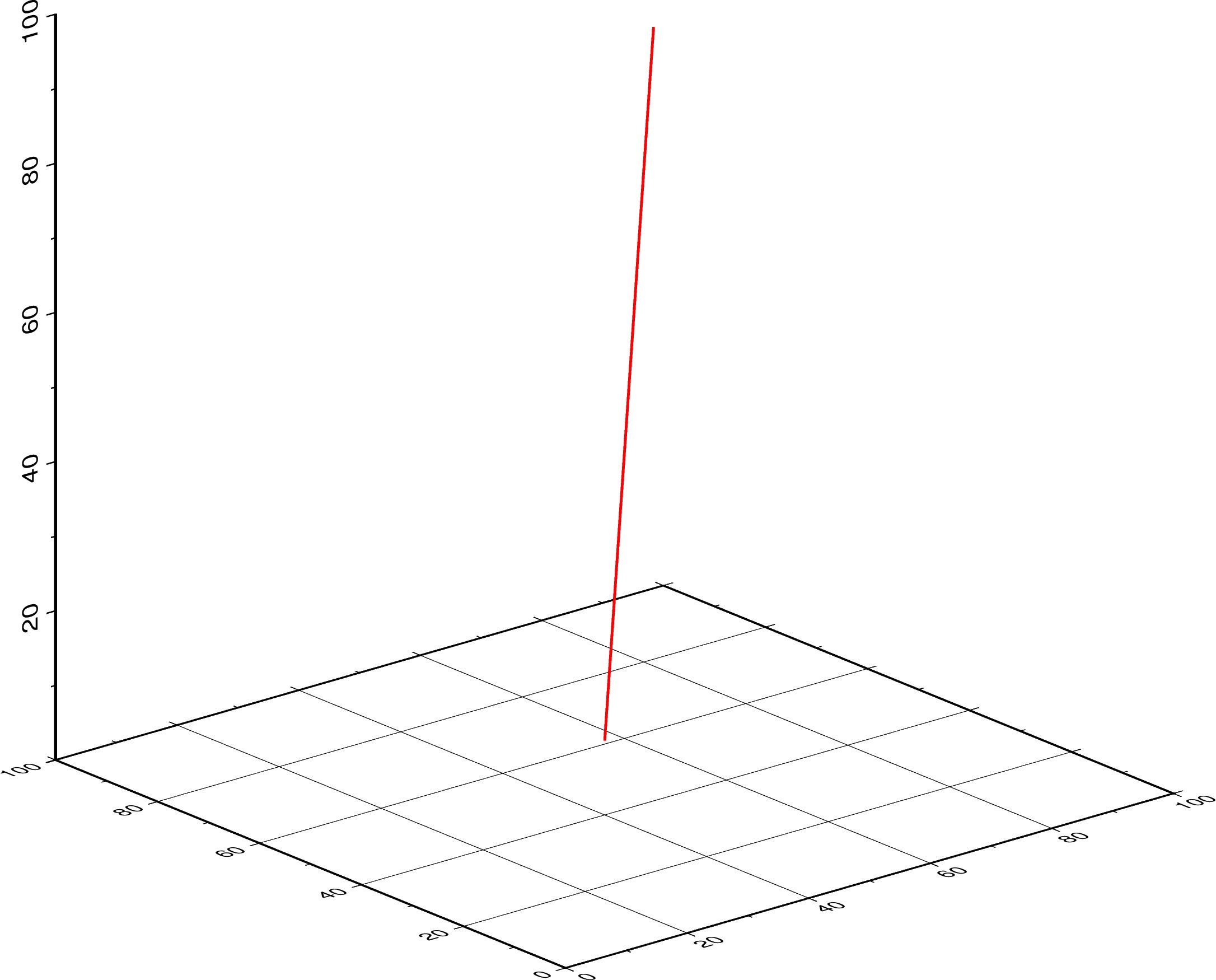
これをプロットするには、gmt plot3d を用いる。 -p を忘れずに。
#!/bin/bash
gmt begin hogehoge jpg
gmt basemap -JX12 -JZ12 -R0/10/0/10/0/10 -Bafg -Bzafg -BWSneZ -p220/20/0
gmt plot3d "./plot.txt" -W0.25 -p
gmt endこの結果が、
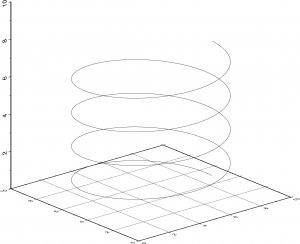
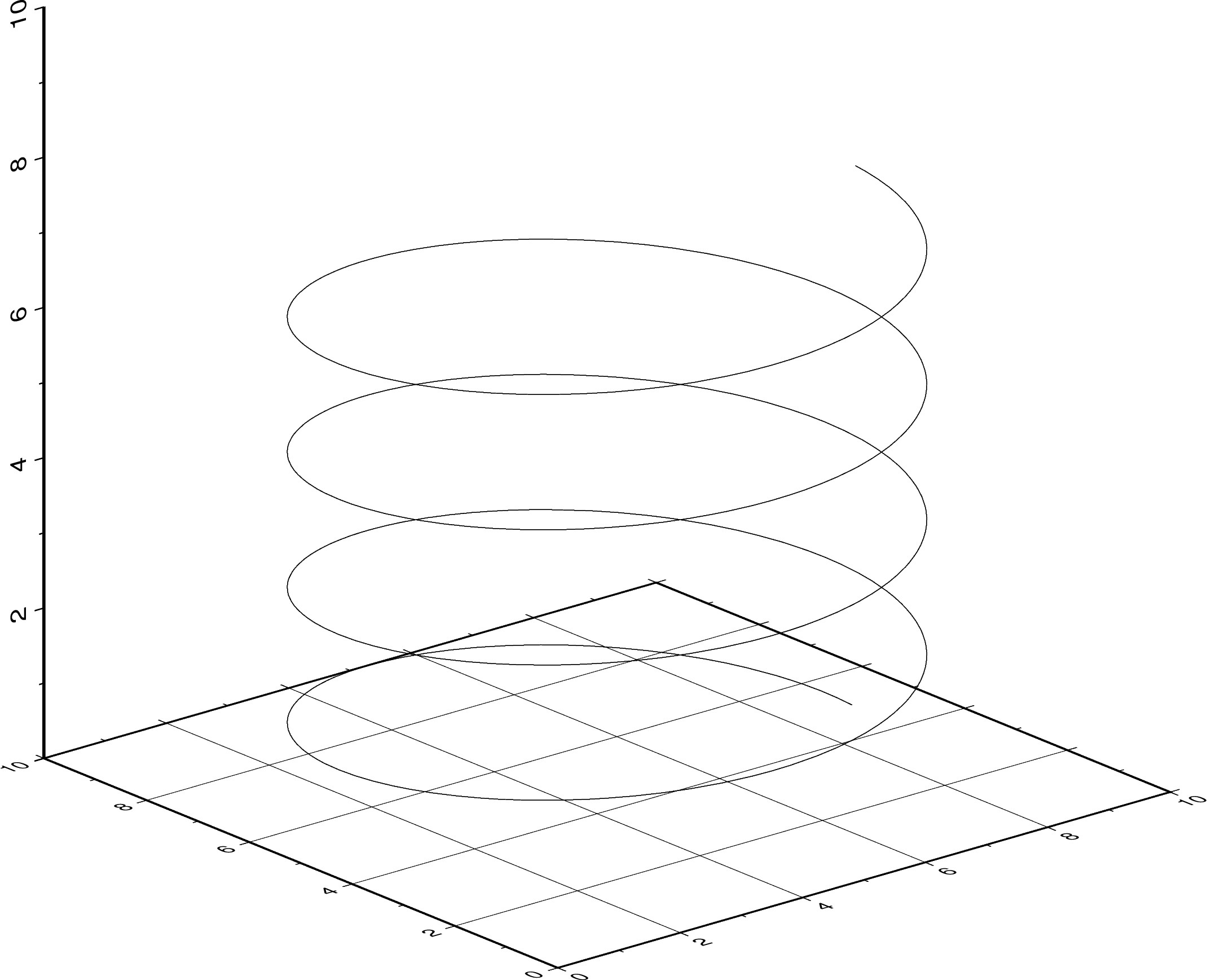
となる。
コメント